Axial Dispersion Large Peclet

Axial Dispersion high peclet number assumption.

class rtdpy.ad_hi_peclet.AD_hi_peclet(tau, peclet, dt, time_end)

Bases: rtdpy.rtd.RTD

Create Axial Dispersion with small amount of Dispersion (Pe>100) Residence Time Distribution (RTD) model. [1]

\[E(t) = \frac{\sqrt{Pe}}{2\tau\sqrt{\pi}} \text{exp}\left[-\frac{Pe \left(1-t/\tau\right)^2} {4}\right]\]

Parameters

tauscalar

L/U. Mean residence time. tau>0

pecletscalar

Reactor Peclet number (L*U/D). peclet>0

dtscalar

Time step for RTD. dt>0

time_endscalar

End time for RTD. time_end>0

References

1

Levenspiel O. (1999) “Chemical Reaction Engineering: Third Edition” John Wiley & Sons, Inc.

Examples

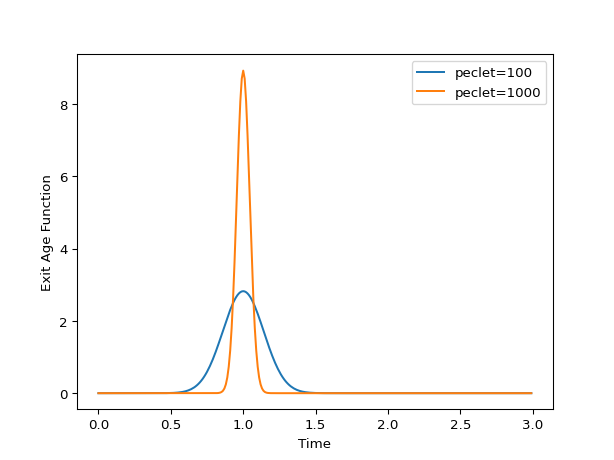
>>> import matplotlib.pyplot as plt
>>> import rtdpy
>>> for pe in [100, 1000]:
...     a = rtdpy.AD_hi_peclet(tau=1, peclet=pe, dt=.01, time_end=3)
...     plt.plot(a.time, a.exitage, label=f"peclet={pe}")
>>> plt.xlabel('Time')
>>> plt.ylabel('Exit Age Function')
>>> plt.legend()
>>> plt.show()

property dt

Time step for RTD

property exitage

Exit age distribution for RTD

property exitage_norm

Normalized Exit Age Distribtion for RTD

frequencyresponse(omegas)

Parameters

omegasndarray

frequencies at which to evaluate magnitude response

Returns

magnitudendarray

frequency magnitude response at omegas

funnelplot(times, disturbances)

Return maximum output signal due to square disturbances.

Uses method from [Garcia] . Also returns meshgrid for times and disturbance inputs for ease of plotting.

Parameters

timesarray_like, size m

Times to determine funnelplot

disturbancesarray_like, size n

Disturbance magnitudes

Returns

x2D meshgrid size (mxn)

times

y2D meshgrid size (mxn)

disturbances

response2D meshgrid size (mxn)

maximum response at (x,y)

References

Garcia

Garcia-Munoz S., Butterbaugh A., Leavesley I., Manley L.F., Slade D., Bermingham S. (2018) A flowhseet model for the development of a continuous process for pharmaceutical tablets: An industrial perspective. “AIChE Journal”, 64(2), 511-525.

integral()

Integral of RTD.

mrt()

Mean residence time of RTD.

output(inputtime, inputsignal)

Convolves input signal with RTD

Parameters

inputtimendarray

Times of input signal, which must have same dt as RTD. Size m

inputsignalndarray

Input signal. Size n

Returns

outputsignalndarrary

Output signal at same dt. Size m + n -1

property peclet

Peclet Number

sigma()

Variance of RTD.

property stepresponse

Step respose of RTD

property stepresponse_norm

Normalized step respose of RTD

property tau

Mean residence time, Tau.

property theta

Dimensionless Time.

property time

Time points for exitage function.

property time_end

Last time point for RTD